はじめに
こんにちー。なたでです。
今日も引き続き勉強会です。これまで、座標系とその変換を学んできました。今回、その計算方法、具体的にはベクトルや行列演算について、どのようにソースコード上で書けばいいか学んでいきましょう。・・・ということで、DirectX、OpenGL、各シェーディング言語の型や計算の特徴をまとめます。
言語ごとのベクトルと行列の演算
主流なエンジンでのベクトルと行列の型の例の紹介と、演算例を確認しましょう。
DirectXのベクトルと行列の計算
D3DXVECTOR4
x, y, z, w成分を持つ横ベクトル
D3DXMATRIX
4行4列の行列
D3DXMatrixMultiply
行列同士の掛け算を行う
計算例
// ベクトル(横ベクトル)の宣言 D3DXVECTOR4 v4 = D3DXVECTOR4( x, y, z, w); D3DXVECTOR4 v3 = D3DXVECTOR3( x, y, z); // 行列の宣言 D3DXMATRIX M = D3DXMATRIX( _11, _12, _13, _14, // row 1 _21, _22, _23, _24, // row 2 _31, _32, _33, _34, // row 3 _41, _42, _43, _44 ); // row 4 // 行列同士の掛け算 A * B = C D3DXMatrixMultiply(&C, &A, &B); // ベクトルのドット積 a・b = c c = D3DXVec3Dot(&a, &b); // ベクトルのクロス積 a×b = c D3DXVec3Cross(&c, &a, &b); // 3次元ベクトルと4x4行列との積 aM = b D3DXVec3TransformCoord(&b, &a, &M)
HLSL(High Level Shading Language)のベクトルと行列の計算
float4
x, y, z, w / r, g, b, a 成分を持つ横ベクトル
float4x4
4行4列の行列
mul
積
計算例
// ベクトル(横ベクトル)の宣言 float4 v4 = float4( x, y, z, w); float3 v3 = float3( x, y, z); // 行列の宣言 float4x4 M = float4( _11, _12, _13, _14, // row 1 _21, _22, _23, _24, // row 2 _31, _32, _33, _34, // row 3 _41, _42, _43, _44 ); // row 4 float4x4 M = float4( _m00, _m01, _m02, _m03, // row 1 _m10, _m11, _m12, _m13, // row 2 _m20, _m21, _m22, _m23, // row 3 _m30, _m31, _m32, _m33 ); // row 4 // 行列同士の掛け算 A * B = C C = A * B; // ベクトルのドット積 a・b = c c = dot(a, b) // ベクトルのクロス積 a×b = c c = cross(a, b) // n次元ベクトルとnxX行列との積 aM = b b = mul(a, M);
補足として成分ごとの演算 (DirectX HLSL)によると、行列のコンストラクターのパッキング順は、常に行優先になるとのことです。
OpenGLのベクトルと行列の計算
GLdouble v[4];
4つの値を持つ縦ベクトル(型はGLfloat / GLdoubleの2種類)
GLdouble M[16];
4行4列の行列(型はGLfloat / GLdoubleの2種類)
glMatrixMode + glMultMatrix
行列同士の掛け算を行う
計算例
// ベクトル(縦ベクトル)の宣言
GLfloat v4[4] = { x, y, z, w };
GLfloat v3[3] = { x, y, z };
// 行列の宣言
GLfloat M[16] = {
m00, m10, m20, m30, // column 1
m01, m11, m21, m31, // column 2
m02, m12, m22, m32, // column 3
m03, m13, m23, m33 // column 4
};
// OpenGL単体では計算には向いていない
// OpenGLでは、あらかじめ設定した行列に対して操作を行うことができる
// 行列同士の掛け算 A * B = C
glMatrixMode(GL_MODELVIEW); // とりあえずモデルビュー変換用の行列で計算する
glLoadMatrixf(A); // A をロードする
glMultMatrixf(B); // A * B
glGetFloatv(GL_MODELVIEW, C) // 計算結果を取り出す
注意点として、縦ベクトルのため行列との掛け算は Mv の順序で計算されます。作成した行列を最終的にベクトルvに対して掛け算をするため、行列を準備する際は、逆の順番で行列同士の掛け算が必要となります。
GLSL(OpenGL Shading Language)のベクトルと行列の計算
vec4
x, y, z, w / r, g, b, a / s, t, p, q 成分を持つ縦ベクトル
mat4
4行4列の行列
計算例
// ベクトル(縦ベクトル)の宣言 vec4 v4 = vec4( x, y, z, w); vec3 v3 = vec3( x, y, z); // 行列の宣言 mat4 M = mat4( m00, m10, m20, m30, // column 1 m01, m11, m21, m31, // column 2 m02, m12, m22, m32, // column 3 m03, m13, m23, m33 // column 4 ); // 行列同士の掛け算 A * B = C C = A * B; // ベクトルのドット積 a・b = c c = dot(a, b) // ベクトルのクロス積 a×b = c c = cross(a, b) // nxX行列とn次元ベクトルとの積 Ma = b b = M * a;
OpenGLのヘルパー関数(glMatrixMode、glMultMatrix)と違って、固定化された行列に対して操作していく必要はありません。行列を掛け算していくときは、次のように1行に1つの掛け算を順番に書くことができます。
// 最後の計算が、aM = b の場合(ベクトルが縦行列なので実際はできない) B = A * B; C = B * C; X = v * C; // 最後の計算が、Ma = b の場合(ベクトルが縦なのでこの書き方できる。) B = B * A; C = C * B; X = C * v;
WebGLのベクトルと行列の計算
標準では用意されていないため、
次のようなJavaScriptライブラリを使用して管理します。(いろいろある)
glMatrix
vec3など、GLSLと似た感覚の型名をもてる(列管理)
Sylvester
古くからある行列用の一般的なライブラリ。WebGLでも拡張jsを追加すれば利用可能(行管理)
多くのライブラリで共通して言えることは、OpenGLと同様に、行列のデータを列でもつことです。この理由は、あらかじめ列で持っていくことで、変換行列を uniformMatrix4fv などでGPU内のシェーダーに、アップロードする際に余計な変換をする必要がないためです。
[0, 1, 2, 3, // 1列目 4, 5, 6, 7, // 2列目 8, 9, 10, 11, // 3列目 12, 13, 14, 15] // 4列目
縦ベクトルと横ベクトルの違い
これまで、DirectXではベクトルは横ベクトルとなって、行列と掛け算するときは、vMとなる。OpenGLではベクトルは縦ベクトルとなり、行列と掛け算するときは、Mvとなることが分かりました。しかも、行列を初期化する際の順序も、行で初期化するのか、列で初期化するのか、混乱してきます。そこで、一度、整理したいと思います。
行列の初期化法について
次のような3×3行列を考えましょう。
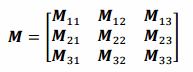
横ベクトルによる計算の場合
DirectXの横ベクトルで演算した場合、次のようになります。
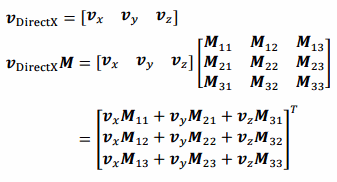
縦ベクトルによる計算の場合
OpenGLの縦ベクトルで演算した場合、次のようになります。
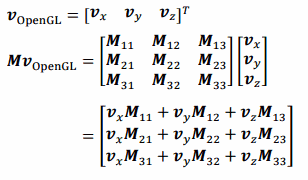
行列の初期化
以上から、ソースコード上、行列を初期化する場合は次のようになります。
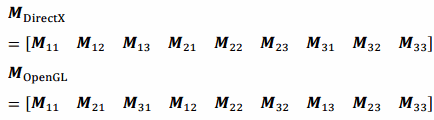
掛け算の順序と行列の初期化について
ここまでまとめると、非常に複雑で混乱しそうです。しかし、よくみると気が付くことがあります。
初期化時の配列の位置と、実際に掛け算したときの結果を色付けしました。
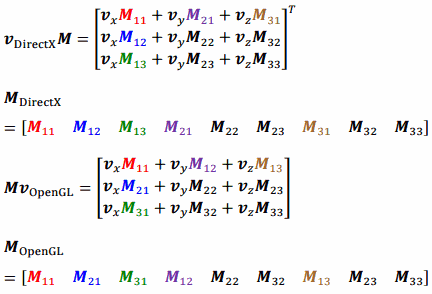
不思議なことに、DirectXとOpenGLとで一見、違いがありません。初期化の順序が異なりますが、掛け算する順序も変わります。そのため最終的には、コード上の見た目の順序でいえば、掛け算の結果は一致するわけです。もちろん、行列同士を掛け算する際は、DirecXとOpenGLとで掛ける順序を気にする必要はありますが、上記のことを知っていると少し混乱がおさまるかとおもいます。(余計混乱を招いたらすみません。)
おわりに
今回は、実際の行列/ベクトル演算の書き方を確認しました。DirectXとOpenGLとで、掛け算をする順序がことなること、行列の初期化方法が異なることが分かりました。ただ、掛け算の順序と行列初期化方法の違いにより、見た目上の掛け算は、一致している部分があることも分かりました。
以上、お疲れ様です。







コメント