はじめに
こんにちは!3DCGの再勉強中のなたでです!
今まで、次の変換行列の違いをみてきました。
本日は変換の最後のビューポート行列の違いを調べてみましょう。ビューポート変換とは、正規化デバイス座標系から、スクリーン座標系への変換となります。前回の講義から、右手座標系・左手座標系という話はなくなっているので、ビューポート行列はDirectX と OpenGL とで同じだと思いますが、どうなんでしょう。
関連記事
DirectXとOpenGLのビューポート行列の定義
DirectXのビューポートの設定
D3DVIEWPORT9構造体でビューポートの定義をして、SetViewportで設定できるようです。
行列というよりは設定値ですね。ちなみにデフォルト値は次のようです。
D3DVIEWPORT9 vp; vp.X = 0; vp.Y = 0; vp.Width = RenderTarget.Width; vp.Height = RenderTarget.Height; vp.MinZ = 0.0f; vp.MaxZ = 1.0f; // vp.X, vp.Y が描写する左上の座標 // vp.Width, vp.Height が描写幅 // vp.MinZ, vp.MaxZ が深度値の変換です
行列は、ビューポートとクリッピング (Direct3D 9)に記載されています。
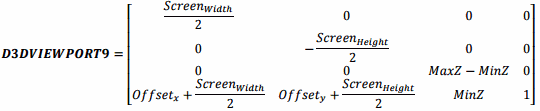
OpenGLのビューポートの設定
OpenGLでも行列というより設定する関数になっています。glViewportとglDepthRangeで直接設定していきます。
void glViewport( GLint x, GLint y, GLsizei width, GLsizei height);
この関数の注意点として、ウィンドウで設定している場合は、左下が原点になります。Windowsの原点は右上で、下に行けばy+にいくのに対して、
glViewportの原点は左下で、上に行けばy+になるわけです。
void glDepthRange( GLdouble nearVal, GLdouble farVal);
描写先の深度値変換の設定です。0 – 1が初期値です。
行列は次のようになります。

参考
ビューポート行列の式の意味
はじめに
これまでのおさらいとなりますが、カメラ座標系から射影トランスフォームをしたものがクリッピング座標系になり、クリッピング座標系から x, y, z を w で割った遠近除算したものが正規化デバイス座標系です。この正規化デバイス座標系から、スクリーン座標系へ変換します。
この正規化デバイス座標系は、次の値の範囲に収まります。
-1 <= x <= 1
-1 <= y <= 1
-1 <= z <= 1 (IF OpenGL)
0 <= z <= 1 (IF DirectX)
この範囲に収まることをふまえて、実際に値をいれながら行列の意味を調べていきます。
値の代入のための式変形
DirectX のビューポート行列の変形
この式が実際にどのようなことをしているか考えてみましょう。
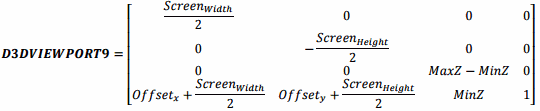
行列の計算は次のようになるので、
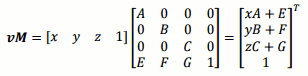
ベクトルに行列を掛け算して、式変形すると次のようになります。
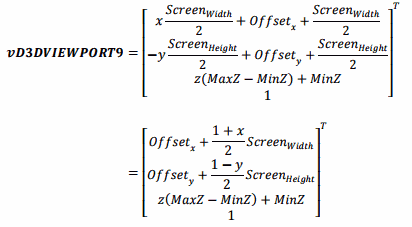
OpenGL のビューポート行列の変形
OpenGLの行列も同様に計算してみましょう。

アスペクト比の補正
x, y, z がとる範囲(-1~1)から、行列の計算によりオフセットの位置から、ウィンドウの幅分へ引き延ばしていることが分かります。ここで、ウィンドウの大きさに引き延ばすからこそ、前回の 射影トランスフォーム行列 にて、ウィンドウのアスペクト比を使用して補正していたのですね。
DirectXとOpenGLのY軸の反転
DirectXでは y が反転しています。これはDirectXの出力先のスクリーン画面では、yが大きいほど下方向に描写されるためです。3D空間上ではもちろん上がプラスなため、ビューポート変換で反転しているわけです。OpenGLの場合は、そもそも出力先のスクリーン画面が上がプラスの設計のため、行列を作っても y の反転は不要となっております。
zの範囲
z については、0がMinZ に 1がMaxZ になるような式になることが分かります。DirectXとOpenGLとで、射影トランスフォーム後の z 値の範囲が異なるため、微妙に式が違っています。実際に計算してあてはめると次のようになります。
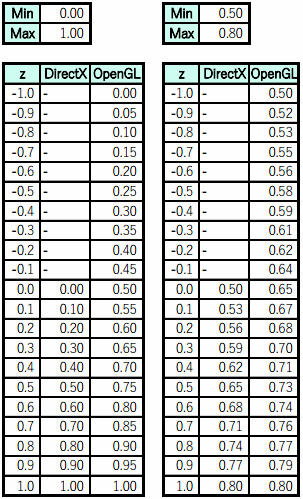
OpenGLでも結局、最終的なz値は 0 <= z <= 1 の範囲に収めているようですね。
なお、この MinZ と MaxZ の設定を利用すると、たとえば、
1度目の描写は、MinZ = 0.0, MaxZ = 0.5
2度目の描写は、MinZ = 0.5, MaxZ = 1.0
のように、1度目の描写の後ろ面に、2度目の描写を行うといったことができます。
おわりに
ここまでのいくつかの回で、3DCGに必要な座標系と、その座標系への変換をまとめました。そして、右手系と左手系、OpenGLとDirectXとで、数式のどこに差が表れてくるのかが分かりました。
これまでDirectXを使っていた方が、WebGL(OpenGL)を始めたい。逆に、WebGLを使っていた方が左手座標系のUnityを使いたいなどがあるかもしれません。そんな時に、これらのまとめを見て、座標系や、DirectX/OpenGLの各変換のこと動きを知っておくと、理解が進みやすいのかなと思います。
以上、ありがとうございました。





コメント