はじめに
こんにちはー!今日は、3D描写するときのテストの話をします。
描写テスト
テストと聞いて何を思い浮かびますでしょうか。試験とか、勉強とかそんなことをきっと思い浮かべるでしょう。作成した3Dポリゴンの頂点を描写するときも、本当に描写していいのか、無駄ではないのか試験をしています。
いくつかテスト方法を紹介しましょう。
背面カリング(裏面カリング)
モデルは多くの3角ポリゴンから構成されています。モデルが回転すれば、裏を向いているポリゴンが出てきます。そんな裏を向いている面を描写しないようにテストします。
クリッピング
視錐台(しすいだい)の中に、ポリゴンが収まっているかどうかテストします。例えば、カメラより手前側にポリゴンが来ていないかといったチェックです。
バウンディングボリュームなど
見えている部分をより特定していく方法です。衝突判定を高速化するためにも使用されます。
今回は、この中でも基本となる裏面カリングの設定方法について解説します。
カリングの仕組み
3Dオブジェクトは、細かな三角形ポリゴンによって構成されています。それは三角形が最も小さな単位だからです。カリングは裏となるポリゴンを描写しない方法なのですが、この三角形の裏と表をどのように決めればいいのでしょうか。
前提条件として、ディスプレイに三角形を表示することを考えます。三角形を構成するためには、3点の座標が必要です。この3点の座標を囲めば、ポリゴンを作ることができるのです。これに対して、裏と表を決める方法は、三角形を結ぶ順番が、時計回りか、反時計回りかで決めればいいのです。そう、決めの問題なのです!
例えば、表向きを時計回りと考えてみましょう。3角形の頂点を裏返した場合は、反時計回りの順序になるので裏と表が分かるわけなのです。
カリングの計算方法
3つの頂点が、時計回りか反時計回りかは簡単に計算できます。
下記の3つの頂点があり、a, b, c の3点を順番に通る三角形を考えます。なお、2次元なので、 x と y 以外は 0 としています。
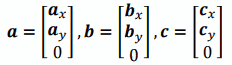
そして、
a, bへ向かうベクトルmを計算します。
a, cへ向かうベクトルnを計算します。
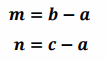
そして、クロス積を行います。計算にはmとnの各ノルムと角度θを使用しますが、ベクトルのまま計算することもできます。なお、a, b, c の3次元目が 0 のため、下記のように簡略化されます。
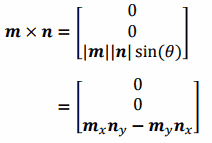
クロス積の結果は、mとnと直行するベクトルです。従って3次元目の成分 z 、直行成分となっており、正負で方向が分かります。

ポリゴンが表か裏かは、意外に簡単に判定できるのです。
カリングの設定方法
各種エンジンでの設定方法をまとめてみます。mk様の算譜記録帳にもまとまっております。
DirectX 9 のカリングの設定方法
次のように、裏面(描写しない面)が時計回りなのか、反時計回りなのかを設定します。つまり、時計回りを表とみなす場合は、D3DCULL_CCWを設定する必要があります。
ソースコード
// 背面のカリングはしません。 SetRenderState(D3DRS_CULLMODE, D3DCULL_NONE); // 三角形の頂点が時計回りならば裏向きと見なし描画しません。 SetRenderState(D3DRS_CULLMODE, D3DCULL_CW); // 三角形の頂点が反時計回りならば裏向きと見なし描画しません。(デフォルト) SetRenderState(D3DRS_CULLMODE, D3DCULL_CCW);
参考
DirectX 11 のカリングの設定方法
FrontCounterClockwiseで表面の定義をして、CullModeで描写しない面の設定が可能です。
ソースコード
// 三角形の頂点が反時計回りならば三角形は前向き FrontCounterClockwise = TRUE; // 三角形の頂点が時計回りならば三角形は前向き(デフォルト) FrontCounterClockwise = FALSE; // 常にすべての三角形を描画します。 CullMode = D3D11_CULL_NONE; // 前向きの三角形を描画しません。 CullMode = D3D11_CULL_FRONT; // 後ろ向きの三角形を描画しません。(デフォルト) CullMode = D3D11_CULL_BACK;
参考
OpenGL のカリングの設定方法
glFrontFaceで表面の定義をして、glCullFaceで描写しない面の設定が可能です。
ソースコード
// 三角形の頂点が時計回りならば三角形は前向き glFrontFace(GL_CW); // 三角形の頂点が反時計回りならば三角形は前向き(デフォルト) glFrontFace(GL_CCW); // 常にすべての三角形を描画します。 glDisable(GL_CULL_FACE); // 前向きの三角形を描画しません。 glEnable(GL_CULL_FACE); glCullFace(GL_FRONT); // 後ろ向きの三角形を描画しません。(デフォルト) glEnable(GL_CULL_FACE); glCullFace(GL_BACK);
参考
おわりに
今回は、描写テストでも基本的なカリングの解説をしました。カリングは計算も簡単で、お手軽に描写負荷を下げることができます。レンダラーを作る方や、頂点とインデックスで構成されたモデルデータのローダーを作成する方などの参考になると幸いです。
では、またね!
関連記事
・3DCGの座標系の紹介
・DirectXとOpenGLの回転行列、回転軸、回転方向
・DirectXとOpenGLのビュートランスフォーム行列の違い
・DirectXとOpenGLの射影トランスフォーム行列の違い
・DirectXとOpenGLのビューポート行列の違い
・DirectXとOpenGLのベクトル/行列演算の違い




コメント