 VRChat
VRChat VRChatのアバターの身長と頭身を調査してみる
はじめにこんにちは。VRoid Studioでアバターを作成することがあるのですが、どれぐらいの身長が適しているか迷うことがあります。そこで今回私がいくつか目にしたアバターの身長について調べてみることにしました。調査するアバターは独断があり...
 VRChat
VRChat  VRChat
VRChat  VRChat
VRChat 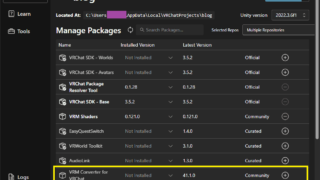 VRChat
VRChat  VRChat
VRChat  VRChat
VRChat  VR
VR  セカンドライフ制作
セカンドライフ制作 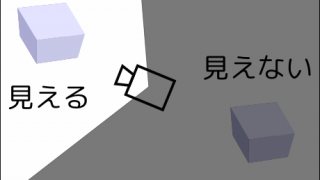 セカンドライフ制作
セカンドライフ制作  ライブラリ制作
ライブラリ制作  CG制作
CG制作 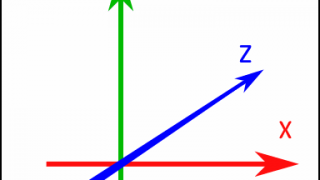 アルゴリズム
アルゴリズム