はじめに
みなさん、こんにちは。
これまで2回にわたって、指定した範囲で乱数を作る方法や、その「罠」について紹介してきました。改めて振り返ると、乱数って意外と奥が深いですね。
読み忘れた方のためにリンクを貼っておきます!
- 指定した範囲の乱数を作る際の罠(前編)
- 指定した範囲の乱数を作る際の罠(後編)
- 指定した範囲の乱数を作る際の罠(実戦編)←いまここ
実例で乱数の“落とし穴”を体感する
はじめに
ここまでの内容を見て、「ビット数の小さい乱数生成器とか、普段はあまり関係ないのでは?」と感じた方もいるかもしれません。でも、実際のアプリやゲーム開発では、この“ちょっとした違い”が意外な落とし穴になることがあります。
今回は短めの記事ですが、具体例を通して乱数の「ありがちなワナ」にハマってみましょう。
ネットワークゲームのレアアイテム確率を考える
例えば、あなたがネットワークゲームを設計しているとします。モンスターを倒したとき、レアアイテムがドロップする確率を0.01%刻みで細かく設定できるようにしたい。使う言語は C または HSP3 を想定したいと思います。
乱数作成も高速化したいし、x = rand() % 10000 で0~9999の値を作って、if(x < 1000) なら10%で成功!
こんな考えで、実際にコードを書いてみましょう。
実際にHSPでやってみる
HSP には rnd(n) という関数がありますが、これはC言語でいう rand() % n と同じです。
#define multiplier 214013 #define addend 2531011 x = 1 goto *start #defcfunc rnd2 int s x = x * multiplier + addend return (((x >> 16) & 0x7FFF) \ s) *start mes "HSPの rnd(n) は、余りを使用して乱数を切り出している。" mes "HSPの rnd -> " + rnd(100) + " は" mes "上記の rnd2 -> " + rnd2(100) + " と同じ。"
このように、rnd(n) も「余り」を使って乱数を作っています。
実際の分布を調べてみる
では、こういった乱数で実際にどのくらい均等な分布になるのか、10万回試して度数分布表を作ってみましょう。
size = 100000
dim bin, 10
repeat size
x = rnd(10000)
bin(int(x / 1000))++
loop
repeat 10
mes strf("[%5d ,%5d) ... %5d回", (cnt * 1000), ((cnt + 1) * 1000), bin(cnt))
loop
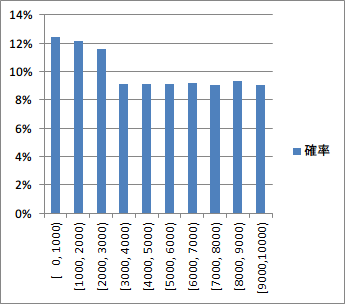
実行してみると、なんと驚きの結果が出ます。
| 範囲 | 回数 |
|---|---|
| [ 0, 1000) | 12401 |
| [1000, 2000) | 12176 |
| [2000, 3000) | 11618 |
| [3000, 4000) | 9079 |
| [4000, 5000) | 9088 |
| [5000, 6000) | 9107 |
| [6000, 7000) | 9150 |
| [7000, 8000) | 9048 |
| [8000, 9000) | 9316 |
| [9000,10000) | 9017 |
if(rnd(10000) < 3000) で30%のつもりが、実際は36%も当たってしまうこともあります。グラフにしてみると、その偏りがよりハッキリ分かります。
より正しい乱数を作るには
さて、こうした問題を避けるにはどうすればいいか?
HSP3でより正しい乱数を作る方法をいくつか紹介します。下記のコードは、ビット数を増やす工夫や、余りが出た場合に再抽選する手法なども盛り込んでいます。
#module
#defcfunc rnd15 int s
// 15ビットの実数の乱数を作成
return int(((double(rnd(0x8000))) / 0x8000) * s)
#defcfunc rnd30 int s
// 30ビットの実数の乱数を作成
return int(((32768.0 * rnd(0x8000) + rnd(0x8000)) / 0x40000000) * s)
#defcfunc rnd52 int s, local a
// 52ビットの実数の乱数を作成
a = double(rnd(0x8000))
repeat 3
a *= 32768
a += rnd(0x8000)
loop
return int(a / 1152921504606846976.0 * s)
#defcfunc rnd4 int s, local a, local b
// 繰り返して範囲外は捨てる
repeat
a = rnd(0x8000)
b = a \ s
if(a - b + s <= 0x8000) {
break
}
loop
return b
#global
font "MS ゴシック", 12
pos 5, 5
// 作成する乱数の範囲によって、
// 乱数のビットを大きいものを選ぶか、
// 上記の rnd4() を利用するといいです。
randomize
size = 1000000
mes "通常版"
dim bin, 10
repeat size
x = rnd(10000)
bin(int(x / 1000))++
loop
repeat 10
mes strf("[%5d ,%5d) ... %5d回", (cnt * 1000), ((cnt + 1) * 1000), bin(cnt))
loop
mes "工夫したもの"
dim bin, 10
repeat size
x = rnd15(10000)
bin(int(x / 1000))++
loop
repeat 10
mes strf("[%5d ,%5d) ... %5d回", (cnt * 1000), ((cnt + 1) * 1000), bin(cnt))
loop
mes "誤差が少ない"
dim bin, 10
repeat size
x = rnd30(10000)
bin(int(x / 1000))++
loop
repeat 10
mes strf("[%5d ,%5d) ... %5d回", (cnt * 1000), ((cnt + 1) * 1000), bin(cnt))
loop
pos 200, 5
mes "最も誤差が少ない"
dim bin, 10
repeat size
x = rnd52(10000)
bin(int(x / 1000))++
loop
repeat 10
mes strf("[%5d ,%5d) ... %5d回", (cnt * 1000), ((cnt + 1) * 1000), bin(cnt))
loop
mes "正しい乱数"
dim bin, 10
repeat size
x = rnd4(10000)
bin(int(x / 1000))++
loop
repeat 10
mes strf("[%5d ,%5d) ... %5d回", (cnt * 1000), ((cnt + 1) * 1000), bin(cnt))
loop
以下が実行結果になります。
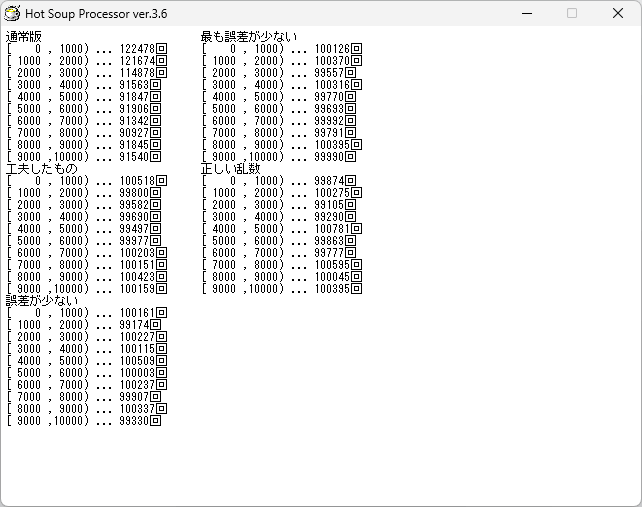
上記の「正しい乱数」のアルゴリズムについては、後編でも説明していますので、興味がある方はそちらも参照してください。
おわりに
今回は、身近なプログラムの例を通じて、乱数の落とし穴について紹介しました。普段あまり意識しない部分ですが、乱数の扱いには十分注意が必要です。
より正確な乱数が必要な場合は、ビット数を増やしたり、余りが出るときは再抽選する方法を選ぶと良いでしょう。もし詳しく知りたい方は、ぜひ前編・後編もあわせて読んでみてください!








コメント