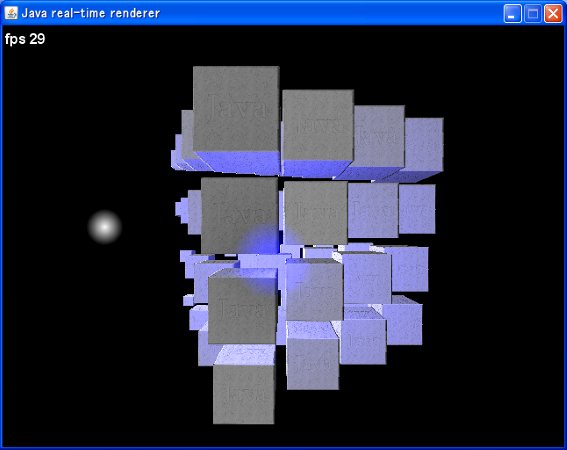
今週は地味なことを。li(A´・ω・)
・ シーンの追加
シーンに表示したいのをまとめてから、シーンをレンダラーに描写っていう感じに。
これによって、レンダリングを、スレッドとして別に走らせたり、
パーティクルや半透明オブジェクトを、最後にZソートして表示とかを自動で出来るようになります。
表示で、対応しているものとして、
「オブジェクト」と「アルファブレンドつきオブジェクト」と「パーティクル」と3種類あります。
というわけで、シーンを描写する際に、
「アルファブレンドつきオブジェクト」と「パーティクル」の2種類をそれぞれクイックソートを行って、
最終的な表示は、「オブジェクト」を表示後に、この問題の2種類をマージソートしながら描写という形にしました。
なんで、2種類をいっきにクイックソートしないのかというと、ただ単にクラスが違う種類になっていたのではい。
今はライトの数・位置は、Rendererクラスに登録する感じになってるのですが、
Sceneクラスに登録できたほうが自然かもしれません。
SceneクラスをRendererクラスに渡すというような。うん。
・ 4×4行列を4×3行列にした。
通常、回転のみの行列は3×3行列で、移動をともなうから4×4行列にします。
しかし、4列目は透視変換を行列に表すときしか使いません。
ということで、透視変換は、行列として一緒にまとめなければ、4×3行列の方が計算やメモリなどの効率がいいです。
4×3行列といっても、回転用の3×3行列と移動用の3×1行列を別々にもっているという感じなので、
逆行列の計算も簡単にできます。ベクトルへの掛け算や行列同士の掛け算は工夫が必要ですが。はい。
・ 回転がおかしい。
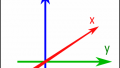
左手系で、DirectXの座標系(上がY軸、奥がZ軸、右がX軸)で作っていたのですが、よくみると回転がおかしい。
具体的には、Y軸の回転は上に向かって時計回り、
Z軸とX軸の回転は、奥に対して、反時計回り、というものです。Σ(・ω・`|||)!!
たしか、本当は軸のむいている方向に対して、時計回りが正しいような。はい。
というわけでビュー行列を久しぶりに触ってなおしてみようと。
3Dネットゲーム製作時代のビュー行列
//視点を原点にする。 this.m_t1.setTranslate(-this.cameraposition.x,-this.cameraposition.y,-this.cameraposition.z); //注視方向をZ軸にする。 double delta_x = this.viewposition.x - this.cameraposition.x; double delta_y = this.viewposition.y - this.cameraposition.y; double delta_z = this.viewposition.z - this.cameraposition.z; this.distance = Math.sqrt(delta_x*delta_x + 【delta_y*delta_y】 + delta_z*delta_z); ←【】はバグ this.m_ry.setRotateY(Math.atan2(-delta_x,delta_z)); this.m_rz.setRotateZ(Math.PI); this.m_rx.setRotateX(Math.atan2(-delta_y,this.distance)); this.distance = 1; //視点位置を(0,0,-r)にする。rの距離だけ離す this.m_t2.setTranslate(0, 0, this.distance); //変換行列をまとめる this.m_first.setMatrix(this.m_t1); this.m_first.mul(this.m_ry); this.m_first.mul(this.m_rz); this.m_first.mul(this.m_rx); this.m_first.mul(this.m_t2);
バージョン2
//視点を原点にする。 this.m_t1.setTranslate(-this.cameraposition.x,-this.cameraposition.y,-this.cameraposition.z); //注視方向をZ軸にする。 double delta_x = this.viewposition.x - this.cameraposition.x; double delta_y = this.viewposition.y - this.cameraposition.y; double delta_z = this.viewposition.z - this.cameraposition.z; this.m_ry.setRotateY(Math.atan2(-delta_x,delta_z)); this.m_rz.setRotateZ(-Math.PI); this.m_rx.setRotateX(Math.atan2(-delta_y,Math.sqrt(delta_x*delta_x+delta_z*delta_z))); this.m_reflection.setScale(-1, 1, 1); this.distance = 1; //視点位置を(0,0,-r)にする。rの距離だけ離す this.m_t2.setTranslate(0, 0, this.distance); //変換行列をまとめる this.m_first.setMatrix(this.m_t1); this.viewmatrix.setMatrix(this.m_ry); this.viewmatrix.mul3(this.m_rz); this.viewmatrix.mul3(this.m_rx); //反転 this.viewmatrix.mul3(this.m_reflection); this.m_first.mul4x3(this.viewmatrix); this.m_first.mul4x3(this.m_t2);
バージョン3
//視点を原点にする。 this.m_first.setTranslate(-this.cameraposition.x,-this.cameraposition.y,-this.cameraposition.z); //注視方向をZ軸にする。 double delta_x = this.cameraposition.x - this.viewposition.x; double delta_y = this.cameraposition.y - this.viewposition.y; double delta_z = this.cameraposition.z - this.viewposition.z; this.m_ry.setRotateY(-Math.atan2(delta_x,delta_z)); this.m_rx.setRotateX(Math.atan2(delta_y,Math.sqrt(delta_x*delta_x+delta_z*delta_z))); this.m_reflection.setScale(-1, -1, -1); //変換行列をまとめる this.viewmatrix.setMatrix(this.m_ry); this.viewmatrix.mul3(this.m_rx); //反転 this.viewmatrix.mul3(this.m_reflection); this.m_first.mul(this.viewmatrix);
うん。
バージョン2からバージョン3へと色々いじったのですが、軸の回転直りませんでした。/(^o^)\
そういえば、
「視点位置を(0,0,-r)にする。rの距離だけ離す」とか習ったけど、これ使わなくていいですね。
あと、「透視変換をZ値にも適用して奥行き情報の保存」とかも習ったけど、実際はZ値に適用しない方がいいです。
え?習った?いえ。なんでもありません。(。・ω・。)ノ
まあ、このままにしておきます。
・ Planeクラス
平面のMeshクラスじゃなくて、平面の当たり判定関係のクラス。
今回作ったのはこれだけ。
・任意の3点から平面を設定
・任意の点から平面への距離
・任意の点から一番近い平面上の点
・v0からv1への線分と、平面との交点
作るにあたって「はじめての3Dゲーム開発」と「実例で学ぶゲーム3D数学」の2冊を参考。
「はじめての3Dゲーム開発」の方は、P285にそのことが書いてあります。
説明は分かりやすいのですが、誤植がとてもひどい。(;-ω-)
2冊のうち、1冊購入するとしたら後者がおすすめ。
次は、3Dマップのクラスの製作にとりかかります。
あれ、何を目指しているんだろう……。
いや、目指しているものはあるんですが、
ここに書いて、できなかったら恥ずかしいので書きません。(´・ω・`)
鎌田 茂雄 はじめての3Dゲーム開発―「DirectX9」の使い方から「1人称3Dフィールド・ゲーム」の制作まで
P284の「これを、tについて解きます。」から、tがTになっている。
すると、P284の「これを、tについて解きます。」の下の式が間違っていることに気づきます。
T = – ( a*x1 + b*y1 + c*z1 + d) / ( a*vx + b*vy + c*vz)
↓
t = – ( a*x0 + b*y0 + c*z0 + d) / ( a*vx + b*vy + c*vz)
このまま、x0とx1が逆になるように式を修正していき、P285で今までの修正式を利用すると、
交差していないときにTRUEを返す式になります。
P285のソースは、修正式から一度式を見直すことで作れるコードで、
これはこれで、正直に利用すれば変なことは起きないと思いますが、
数式の流れからみるとソースコードはおかしなことになると思います。
また、P285は交点を求める関数と書いてありますが、コードのとおり交差を調べる関数です
交点を調べるには、fTを利用する必要があります。






コメント