セカンドライフで見ていないときに動く物体を作る

セカンドライフ制作
スポンサーリンク

はじめに

こんにちはー。

セカンドライフ技術系 Advent Calendar 2018の1日目のなたでです。sabro様、お忙しいにもかかわらずこのような場を毎回準備していただきありがとうございます。去年は忙しく参加できませんでしたが、今年は参加してみたいと思います！

さて、今年2018年ですが、カレンダーを誰も埋めていないのです！これはかなり危険な状況！？11月30日になってもだれもカレンダーを埋めていなくて、とっとりあえず1日目埋めました……！たぶん、また記事を途中で追加したいと思います。みなさんも埋めましょう（笑）

今日は、目で見えていないときにだけ動く物体を作るにはどうすればいいか、ちょっと考えてみたいと思います。・・・え？なぜそんなもの作りたい？ほら、「だるまさんがころんだ」みたいなオブジェクトを作ったりしたい場合はどうすればいいのかなーとなんとなく気になったからです！

アルゴリズム

条件を考える

一番大事なのがアルゴリズムなのですが、この物体が見えているか、見えていないかというのは、奥が深いのです。

こんなのを作れればベストなのですが、

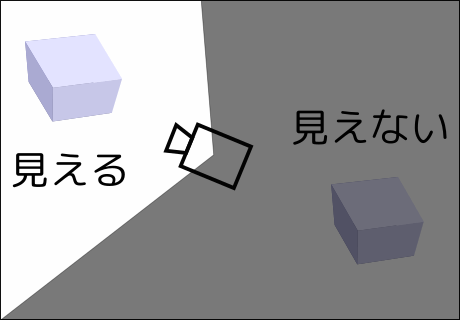
しかし、上記のスクリプトは問題があります。実は、セカンドライフのスクリプト上からは、カメラのFOV（Field of View）情報と、ゲームスクリーンのサイズ情報が取得できないのです。

FOVは、視野角（大きいと広く写せられる値）を表しており、セカンドライフのデフォルトは60度となります。しかしこれは設定で変更ができます。また、ウィンドウサイズが分からないと正確な画面のアスペクト比が求められないため、正しい座標が分からない問題が発生します。

というわけで、今回は次のように単純化して考えてみます。

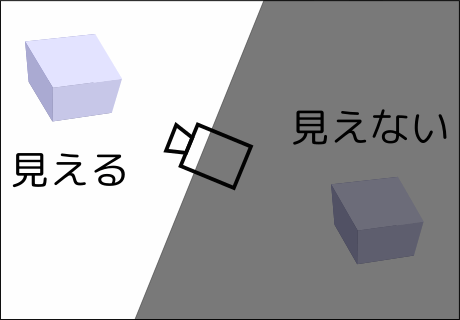
さらに、もっと問題を単純化します。

  1. カメラは、自分のビューアのカメラ情報のみを考慮する。
  2. 物体の大きさは考慮せず、物体の中心座標がカメラの中に入るかどうかで考える。

1.の理由は、スクリプトから他人のビューアのカメラ情報を取得することができないためです。

2.の理由は、これも問題を単純化するためです。

数式を考える

今回、単純化したことにより「カメラから物体が見えるか見えないか」は、「ある定義した平面から、物体までの距離を測って判定する」というシンプルな問題になります。シンプルとは言っても通常、三角関数やら、行列やら非常に複雑なイメージをする方がいるかもしれません。実は、幾何学的な計算を用いると単純な計算で求められる場合があります。というのも、2次元平面上でベクトルを利用した計算が、3次元空間上でも通用する場合があるためです。

まず平面の形式は、2つの値のみで表すことができます。具体的には、面が向いている法線ベクトルnと、原点からの面までの距離dです。これは、カメラの位置pと、カメラの向きvがあった場合、以下の式で求められます。

$$\vec{n}=\vec{v}, d=\vec{v}\cdot\vec{p}$$

この平面情報nとdがあった場合に、物体の中心座標Xと平面との距離distanceは以下の式で求められます。

$$distance=\left(\vec{X}\cdot\vec{n}\right) – d$$

上記の式は2次元平面で成り立つ式ですが、3次元空間上でも通用します。幾何学は面白いですよね。興味がある方は、ほかの計算例として私が書いた「セカンドライフでジャンプ台を作る」も観ると楽しいかもしれません。ちなみに、もっと知りたい方は「O’Reilly Japan – 実例で学ぶゲーム3D数学」で勉強できます。

実例で学ぶゲーム3D数学
created by Rinker

プログラム

指針が決まったので、LSLでスクリプトを書いていきましょう。

スクリプト

// 安全カウンター
float die_time_sec = 300.0;

// チェックする頻度
float check_interval_sec = 0.2;

// ワープする頻度
float warp_interval_sec = 3.0;

// ワープできる距離
float warp_distance = 1.5;

// 最も近づく距離
float back_distance = 1.5;

// 置いたかどうか
integer is_rez = FALSE;

integer anzen_counter;

// ベクトルの正規化
vector normalziedVector(vector v) {
	float b = llSqrt(1.0 / (v.x * v.x + v.y * v.y + v.z * v.z));
	return <v.x * b, v.y * b, v.z * b>;
}

// AからBに向かうベクトル
vector getDirection(vector v1, vector v2) {
	return < v2.x - v1.x, v2.y - v1.y, v2.z - v1.z>;
}

// カメラの後ろ側に回り込む
warpToTheBack() {
	vector target_position;
	rotation target_rotation;
	vector my_position = llGetPos();
	vector camera_position = llGetCameraPos();
	rotation camera_rotation = llGetCameraRot();
	
	// 少し後ろの座標を計算
	vector camera_position_back = camera_position + < - back_distance, 0, 0 > * camera_rotation;
	
	// 今の位置から行きたい場所までの方向
	vector direction = getDirection(my_position, camera_position_back);
	
	// 少し移動
	my_position += normalziedVector(direction) * warp_distance;
	
	// 自分がいる方向に体を向ける
	{
		vector euler = llRot2Euler( camera_rotation );
		target_rotation = llEuler2Rot(<0.0, 0.0, euler.z>);
	}
	
	// 地面の上に立たせる
	{
		// 少し上から下に探索
		vector start = my_position + <0, 0, 2>;
		vector end = my_position + <0, 0, -10>;
		list results = llCastRay(start, end, []);
		if(0 < llList2Integer(results, -1)) {
			// 地面の上に設置する
			vector size = llGetScale();
			target_position = llList2Vector(results, 1) + <0.0, 0.0, size.z * 0.5>;
		}
		else {
			// その場に設置する
			target_position = my_position;
		}
	}
	
	// 変更
	llSetPos(target_position);
	llSetRot(target_rotation);
}

integer isSetPermission() {
	integer permissions = llGetPermissions();
	return (permissions & PERMISSION_TRACK_CAMERA) != 0;
}

// カメラが私を向いているかどうか
integer isNotLookMe() {
	if(!isSetPermission()) {
		return FALSE;
	}
	{
		// 座標を取得
		vector camera_position = llGetCameraPos();
		vector camera_normal = <1, 0, 0> * llGetCameraRot();
		vector my_position = llGetPos();
		
		// 平面情報を作成
		vector plane_normal = camera_normal;
		float plane_distance = camera_normal * camera_position;
		
		// 平面からの距離を取得
		float camera_distance = my_position * plane_normal - plane_distance;
		
		return camera_distance < 0.0;
	}
}

check() {
	// 地面にレズしたもので、私を見ていないとき・・・
	if(is_rez) {
		if(isNotLookMe()) {
			float time = llGetTime();
			if(time > warp_interval_sec) {
				llResetTime();
				warpToTheBack();
			}
		}
	}
}

init() {
	llResetTime();
	if(!isSetPermission()) {
		llRequestPermissions(llGetOwner(), PERMISSION_TRACK_CAMERA);
	}
	anzen_counter = (integer)(die_time_sec / check_interval_sec);
}

default {
	
	state_entry() {
		llResetTime();
		llSetTimerEvent(check_interval_sec);
		init();
	}
	
	timer() {
		// 常に設置してあった場合は削除する（行方不明防止）
		anzen_counter--;
		if(anzen_counter <= 0) {
			llDie();
		}
		check();
	}
	
	on_rez(integer param) {
		// 1 ログイン、装備、rez
		is_rez = TRUE;
		init();
	}
	
	attach(key attached) {
		if(attached) {
			// 2 ログイン、装備
			if(llGetTime() < 1.0) {
				is_rez = FALSE;
			}
		}
	}
}

工夫点

  • カメラの位置を調べるために必要なパーミッション情報を確認している
  • 地面に設置したかどうかを判定して、地面に設置したら動作するようにした※
  • リアルにするために少しずつ近づくようにした
  • 物体が浮かばないように、llCastRayを使用して地面の上に設置するようにした
  • 行方不明防止のため、llDieを使用した安全用の削除機能をつけた

※中のスクリプトを上書き保存した場合は、is_rezフラグが経っていないため、置きなおしが必要です。

モデリング

せっかくなので、メタセコイアを使ってモデルも作ってみたいと思います。「だるまさんがころんだ」なので、「だるま」さんっぽいモデルにしてみます。

おおざっぱにつくる

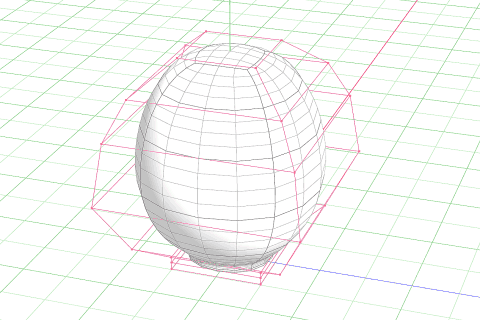
綺麗な球形で作るために、曲面制御（OpenSubdiv）の設定で大雑把に作るのがコツです。

フリーズして整える

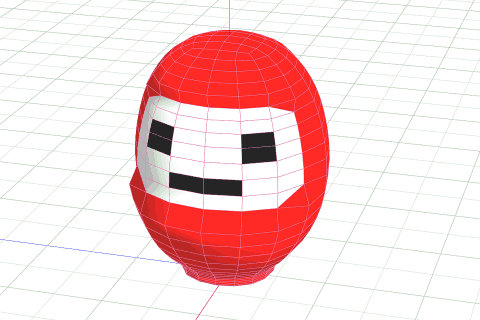
曲面のままだと細かいところで加工がしにくいため、いったん曲面のフリーズをして、スムージングされた頂点を確定させます。その後は、凹ましたり、面への色付けをしていきましょう。

頂点を増やしてディテールを調整する

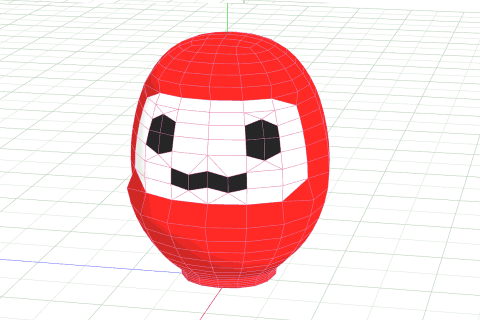
ポリゴンを構成する線に対してナイフを使って頂点を作成します。一旦面を削除して、新たに作成した頂点を利用して面を引き直し、頂点の位置を微調整したら完成です。ちなみに完成してから気が付いたのですが、こういう左右対称のモデルは一旦半分に切ってミラー反転で作成したほうが楽です。

COLLADA形式（dae）で出力しアップロード

あとは、これをdaeファイルで出力し、セカンドライフでアップロードします。出力する際は、セカンドライフ上の軸に合うように、X軸の＋が正面。Y軸の＋が左側。Z軸の＋が上側のように物体を回転させて調整しましょう。詳細を知りたい方は、「セカンドライフでモデリング（メタセコイア編）」を参考にどうぞ。

最終仕上げ

セカンドライフでモデルを置き、回転角度の調整と、面への色付け、スクリプトの入れ込みが終われば完成です。

使用例

実際に上のスクリプトとモデルを使用して、動作させたときの使用例です。

おわりに

おつかれさまです～。

と、とりあえず1日目は無事終わったのですが、今年の Advent Calendar どうなるのでしょうね～。まあ埋まっても、埋まらなくてもみなさん気楽に楽しんでいきましょう～。

スポンサーリンク

コメント

タイトルとURLをコピーしました