はじめに
はじめまして。
「セカンドライフ技術系 Advent Calendar 2015」の12月10日(木)担当の なたで です。
今回、初めての参加ですがよろしくお願いします。
今日は、セカンドライフでジャンプ台のオブジェクトを作ります。
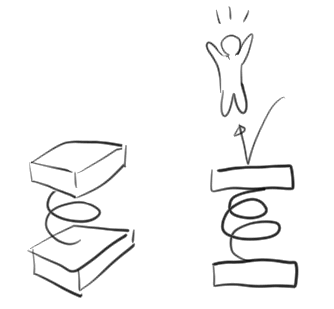
上から乗るとぼよーんとするジャンプ台です。
解説の要点
- ジャンプ台のバネの部分を、Metasequoia でモデリングしよう
- ジャンプ台の上から押したときにだけ、ぼよーんとするスクリプトを書こう
ジャンプ台のバネの部分を、モデリングしよう
Metasequoia を作ってモデリングしていきます。
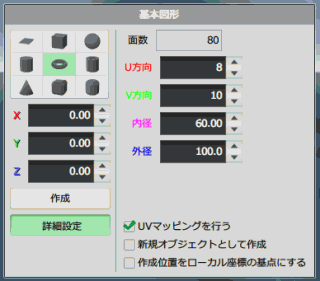
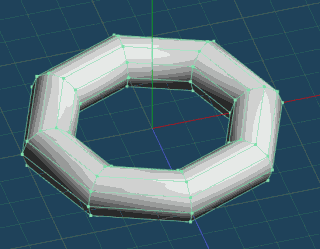
ドーナッツ型の基本図形からバネを作成していきます。
細かいほうが綺麗に作れますが、単純化のために8角形でいきます。
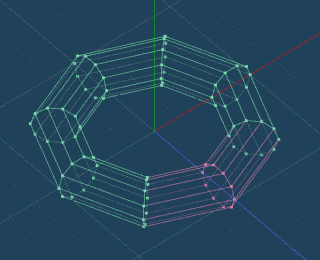
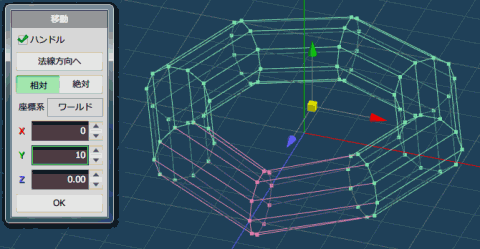
8角形のうち、7つの角を選択して、上に 10 上げます。
複数の選択は、Shiftを押しながら選択でするとできます。
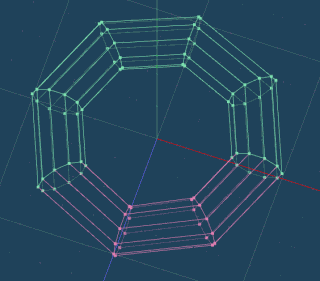
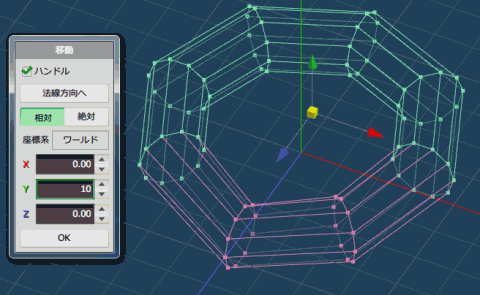
先ほど選択した 7つの角のうち、端っこの選択を解除して、上に 10 上げます。
解除は、Ctrlを押しながら選択すると解除できます。
端から 1 つずつ選択を解除しては 10 上げる作業を繰り返していきます。
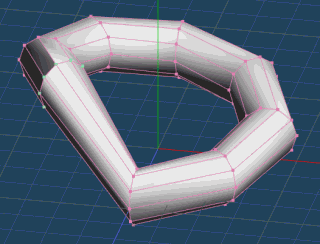
これで、すこしラセンっぽくなりました。
この形をたくさんつなげれば、バネができそうです。
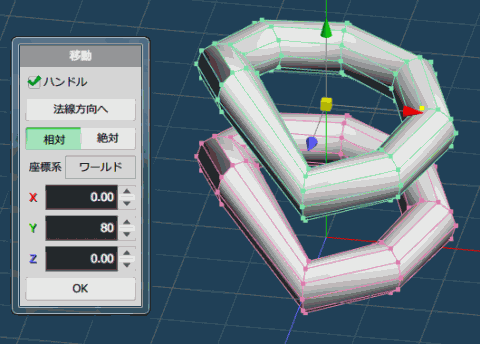
2回転にするために、上にコピーしましょう。
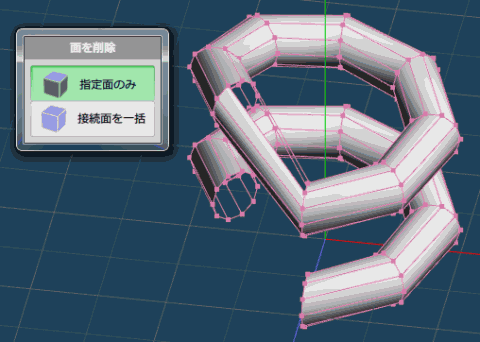
段差が変な部分の面を削除して、
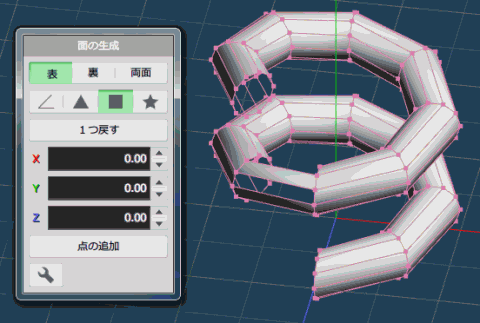
上下のラセンのオブジェクトの断面を、面を繋げていきます。

これでバネが完成しました。
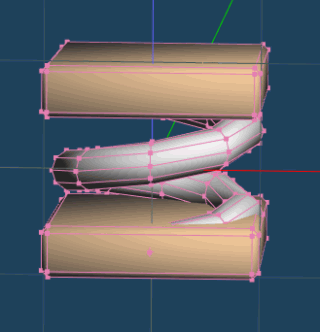
あとは、木のような台を上下にくっつけて、ジャンプ台のモデルは完成です。
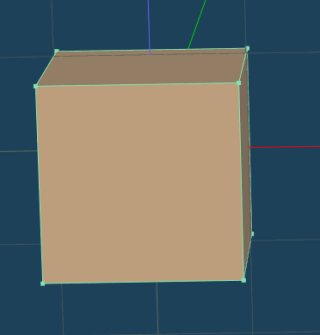
物理判定用のオブジェクトは適当に立方体で作成しておきます。
なお、この時点で、セカンドライフ上の軸と合うように回転させておきましょう。
右が赤のX座標。前が緑のY座標。上が青のZ座標です。
(→詳しくは、 軸についての記事 )
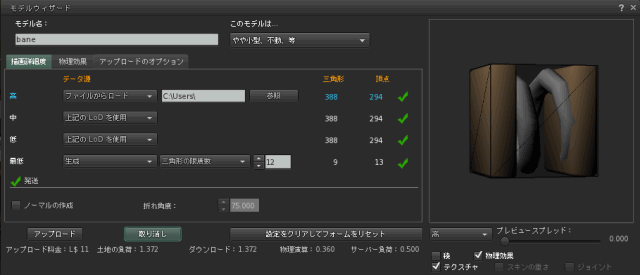
これをアップロードします。
アップロード直後は、
プレビューのように予め初期値で回転されているので、回転をもどして…

できました。
ジャンプ台のスクリプトを書こう
ジャンプ台のスクリプトを書いていきます。。
衝突時の判定は「collision_start」を使用するとよさそうです。
衝突したアバターを、指定した方向へ「llPushObject」で飛ばせばいいのです。
(※土地の設定を、プッシュ許可にしておくこと)
上記の関数を使って「衝突したアバターを、上へ飛ばす」プログラムを書いていくのですが、
単純に実装しようとすると、いくつか問題があることに気がつきます。
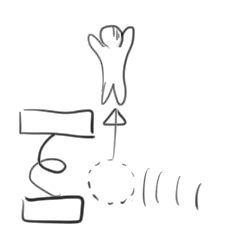
左右からジャンプ台にぶつかった場合でも上へ飛んでしまうのでは?
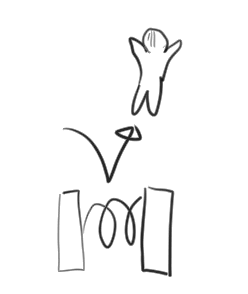
ジャンプ台が傾いていた場合に、上から踏んだ場合はどのようにすれば?
……などなど。
解決策
上記のあらゆる問題を解決するために、ジャンプ台で飛ばす方向に対して、
衝突したアバターの「めり込み具合」を調べて、正しく判断させようと思います。
今回は、ベクトルの計算が必要です。
ベクトルというのは、(x, y, z)など、たくさんの値をもつデータのようなものです。
なお、通常の1つしか値ない場合は、スカラーと呼びます。
今回は2種類のベクトルを使用します。
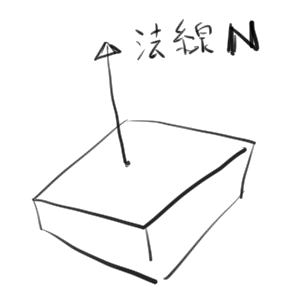
1つ目に、法線ベクトルがあります。
法線ベクトルは、物体の表面から垂直に伸びたベクトルです。
今回は、バネの向いている方向を、法線ベクトルとして考えたいと思います。
このベクトルは N と呼び、長さ(ノルム)を1とし、単位ベクトルとします。
なお、長さを1にすることで、純粋に方向のみを表すことができます。
よく使用するテクニックなので覚えておくといいかもしれません。
具体的には、「ベクトル」÷「ベクトルの長さ」の計算をすると、長さを1にできます。
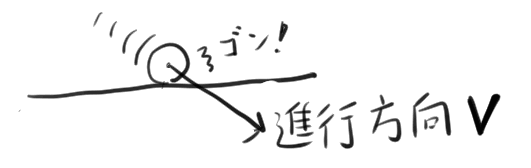
次に、速度ベクトルVです。
衝突したオブジェクトがどの方向へどの速度で向かっているかとなります。
方向はオブジェクトが向かっている方向、長さは速度に相当します。
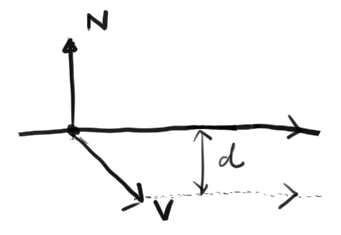
衝突したある点からの法線ベクトル N と、衝突時の速度ベクトル V があったときに、
このめり込み具合 d の長さを計算します。
実は、簡単に計算ができる方法あります。
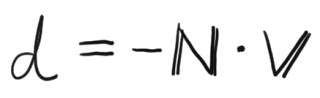
こんな式です。
こんな計算で、dが求められるのと思うかもしれませんが、求められます。
ベクトル同士を「・」すると、内積となり、
細かいことはおいておいて、dが求まります。
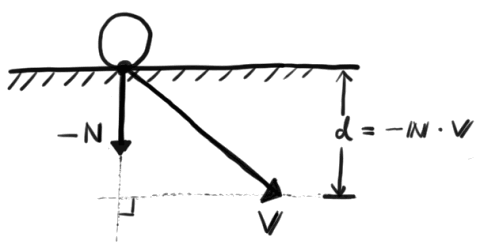
Nが単位ベクトル(長さ=1)となっているところがポイントです。
すこし難しいですが、ベクトルVを、単位ベクトルであるNに射影したベクトルのノルムが内積となります。
さて、スクリプトは次のようになります。
integer i;
list get_details = [ PRIM_SIZE, PRIM_POSITION, PRIM_ROTATION ];
vector object_size = <0, 0, 0>;
vector object_position = <0, 0, 0>;
rotation object_rotation = <0, 0, 0, 1>;
vector target_velocity = <0, 0, 0>;
vector object_normal = <0, 0, 0>;
vector object_normal_inv = <0, 0, 0>;
vector refrect_vector = <0, 0, 0>;
// 設定値
float power = 3.0; // 少しの力でもある程度飛ばす
float rebound = 2.0; // 何倍の力で戻すか
float threshold = 0.5; // この閾値より低いと吹き飛ばさない
getData() {
list list_details = llGetPrimitiveParams(get_details);
object_size = llList2Vector(list_details, 0);
object_position = llList2Vector(list_details, 1);
object_rotation = llList2Rot(list_details, 2);
object_normal = <0, 0, 1> * object_rotation; // バネの上の向きベクトル
object_normal_inv = <0, 0, -1> * object_rotation; // バネの下の向きベクトル
}
onStartCollision(integer num_detected) {
// 使用するオブジェクトのデータの取得
getData();
// めり込み度を計算(内積)
float merikomi = target_velocity * object_normal_inv;
// あまり押されていなかったら、処理しない
if(merikomi < threshold) {
return;
}
// 跳ね返すベクトル
refrect_vector = (object_normal * (llFabs(merikomi) + power) ) * rebound;
// プッシュ!
for(i = 0; i < num_detected; i++) {
llPushObject(llDetectedKey(i), refrect_vector, <0, 0, 0>, FALSE);
}
// オブジェクトが一瞬縮んで、押された感じにする
vector object_position_new = object_position + object_normal_inv * (object_size.z * 0.5);
vector object_scale_new = <object_size.x, object_size.y, object_size.z * 0.5>;
llSetScale(object_scale_new);
llSetPos(object_position_new);
llSleep(0.1);
llSetPos(object_position);
llSetScale(object_size);
}
default {
collision_start(integer num_detected ) {
// 即速度を取得しないと、止まった時の速度を取得してしまう
target_velocity = llDetectedVel(0);
// 後はこの中で処理
onStartCollision(num_detected);
}
}
以上、「ジャンプ台を作る」の解説を終えます!
お疲れ様でした!





コメント